Market stage detection with Python and Pandas
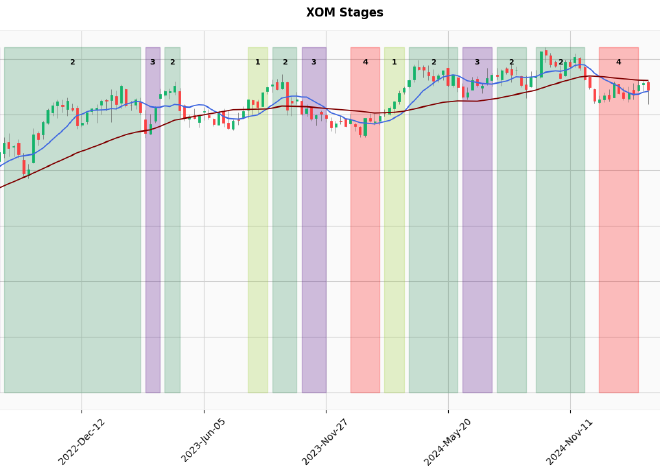
Table of Contents
Market stage detection helps you make more informed trading decisions and understand where a stock currently sits in its market cycle.
Let’s learn how we can apply market stage detection to our trading algorithms.
This tutorial is part 7 in a larger series on getting started with fintech and market analysis with Python:
- How to download market data with yfinance and Python
- Rethinking yfinance’s default MultiIndex format
- How to plot candlestick charts with Python and mplfinance
- How to compute Simple Moving Averages (SMAs) for trading with Python and Pandas
- Finding consecutive integer groups in arrays with Python and NumPy
- Computing slope of series with Pandas and SciPy
- Market stage detection with Python and Pandas (this tutorial)
- Implementing TradingView’s Stochastic RSI indicator in Python
- Introduction to position sizing
- Risk/Reward analysis and position sizing with Python
Configuring your development environment #
Before we dive in, let’s set up our Python environment with the packages we’ll need:
$ pip install numpy scipy pandas yfinance matplotlib mplfinance seaborn
These packages include:
numpy/scipy: Mathematical operations, linear regression for slope calculationspandas: Data manipulation, time series handling, and analysisyfinance: Yahoo Finance API wrapper to download market datamatplotlib/mplfinance: Data visualization and candlestick chartingseaborn: Enhanced visualization capabilities
What are the four market stages? #
Originally described by Stan Weinstein in his 1998 book, Secrets for Profiting in Bull and Bear Markets, the four market stages provide a framework for understanding where a stock is in its cycle:
- Stage I (Accumulation): The bottoming pattern after a downtrend where smart money begins accumulating
- Stage II (Uptrend): The profitable advance phase with higher highs and higher lows
- Stage III (Distribution): The topping pattern where smart money begins distributing their holdings (i.e., sell offs, high volatility, etc.)
- Stage IV (Downtrend): The decline phase with lower highs and lower lows
Stage I: Accumulation #

The accumulation phase occurs after a prolonged downtrend when a stock is building a base.
During this stage:
- The downward momentum has stopped
- Price moves sideways in a trading range
- Volume may increase on up days (showing accumulation)
- The 10-week moving average begins to flatten, then turn upward
- The 40-week moving average is still declining or flat
This period represents smart money beginning to accumulate shares at favorable prices while most retail investors remain pessimistic.
Stage II: Uptrend #

The uptrend phase is where the real profits are made.
In this stage:
- Price breaks above the Stage I basing pattern on increased volume
- The 10-week moving average crosses above the 40-week moving average
- Both moving averages are trending upward
- Price consistently trades above both moving averages
- Higher highs and higher lows form on the chart
This is the ideal time to be invested in a stock—when it’s showing sustained momentum to the upside.
Stage III: Distribution #

The distribution phase represents the topping process.
Key characteristics of this stage include:
- Price movement becomes more volatile and choppy
- The 10-week moving average begins to flatten or turn down
- The 40-week moving average is still rising but flattening
- Volume may increase on down days (showing distribution)
- Failed breakouts are common
This period represents smart money distributing (i.e, selling) their shares to eager retail investors who are late to the party, thinking the Stage II uptrend will continue forever.
Stage IV: Downtrend #

The downtrend phase is where capital preservation becomes critical.
During this stage:
- Price makes lower highs and lower lows
- The 10-week moving average crosses below the 40-week moving average
- Both moving averages are trending downward
- Price consistently trades below both moving averages
- Rallies typically fail at or below the declining moving averages
This is the time to avoid the stock or consider short positions if your strategy permits.
Variations in our market stage detector #
The original method by Weinstein used weekly 10 and 30MA but I use the 10 and 40MA here because I find the 40MA a bit more reliable (i.e., my personal preference).
Additionally, the 40MA is often used by other traders as a major level of support/resistance.
Implementing Stan Weinstein’s market stage detector #
Let’s create a Python implementation of Weinstein’s famous market stage detection system.
We’ll start by importing the necessary packages:
# import the necessary packages
from typing import Optional
from typing import Union
from typing import Sequence
from typing import Tuple
from typing import List
from typing import Dict
from enum import Enum
from numpy.typing import ArrayLike
from dataclasses import dataclass
from datetime import timedelta
from datetime import datetime
from scipy import stats
from matplotlib import patches
import matplotlib.pyplot as plt
import mplfinance as mpf
import yfinance as yf
import pandas as pd
import numpy as np
Key packages include:
pandas/numpy: For data manipulation and calculationsmatplotlib/mplfinance: For creating visualizations of market stagesyfinance: For downloading historical market datascipy.stats: For calculating slopes of moving averages
Helper method to find groups of consecutive integers #
In order to identify what stage a given symbol is in, we need to compute MAs and then measure how long the symbol has exhibited Stage I, Stage II, Stage III, or Stage IV characteristics.
The following helper method finds consecutive groups of integers, which helps us:
- Filter out false positives by requiring a minimum sequence length
- Determine how long a given stage has been ongoing
- Identify if a stage is just starting (potentially a false signal)
- Confirm if a stage is well-established (more reliable for trading)
- Detect if a stage has been ongoing for too long (potential reversal coming)
This method was originally detailed in part five of this series, but it’s included here for completeness:
def find_consecutive_integers(
idxs: Union[ArrayLike, Sequence[int]],
min_consec: int,
start_offset: int = 0
) -> List[Tuple[int, int]]:
# check to see if the indexes input is empty
if len(idxs) == 0:
# return an empty list
return []
# ensure the indexes are an array, then initialize a list to store the
# groups
idxs = np.array(idxs)
groups = []
# find boundaries in consecutive sequences where the difference between
# consecutive elements is *not* one, then add in the start and ending
# indexes to the boundaries
boundaries = np.where(np.diff(idxs) != 1)[0] + 1
boundaries = np.concatenate(([0], boundaries, [len(idxs)]))
# loop over the boundary ranges
for i in range(0, len(boundaries) - 1):
# grab the start and end index of the boundary
start_idx = boundaries[i]
end_idx = boundaries[i + 1] - 1
# check to see if the length of the group is greater than our minimum
# threshold
if end_idx - start_idx + 1 >= min_consec:
# update the list of groups
groups.append((
int(idxs[start_idx]) + start_offset,
int(idxs[end_idx]) + start_offset
))
# return the groups
return groups
The function takes an array of integers (indices where a condition is true), finds consecutive sequences, and returns only those sequences that meet a minimum length requirement.
In the context of market stage detection, we’ll use this method to count the number of consecutive days a given stage has gone on for, allowing us to weed out false positive detections, and measure trend strength.
Helper method to compute slope of values in a series #
To identify market stages, we need to compute the slope of our moving averages.
The slope tells us whether a moving average is trending up, down, or flattening—crucial information for determining the market stage.
We’ll use our handy calculate_slope method to help us:
def calculate_slope(series: pd.Series) -> float:
# check to see if less than two points were provided
if len(series) < 2:
# return NaN since slope cannot be computed
return np.nan
# check to see if performing linear regression would cause a division by
# zero error, including (2) *any* of the data points in the series being
# NaN, or (2) *all* values in the series being equal
if series.isna().any() or np.all(series == series.iloc[0]):
# return NaN
return np.nan
# compute and return the slope for the input data points
return stats.linregress(np.arange(0, len(series)), series).slope
This function calculates the slope of a series using linear regression, providing proper error handling for edge cases.
Implementing our market StageDetector class #
Let’s start by defining an Enum for each of the four market stages:
class Stage(Enum):
# define the stage names
STAGE_I = "stage_1"
STAGE_II = "stage_2"
STAGE_III = "stage_3"
STAGE_IV = "stage_4"
def integer_value(self, sep: str = "_") -> int:
# return the integer value of the stage
return int(self.value.split(sep)[-1])
def __str__(self):
# return the string value
return self.value
The Stage enum defines our four market stages, with helper methods to extract the integer value and string representation for each stage.
Then we’ll define a custom type for our detected stages:
# define a custom type for the detected stage ranges where the key is the
# stage name and the value is a list of 2-tuple integers (i.e., the start
# and end indexes for each range belonging to the stage)
DetectedStages = Dict[Stage, List[Tuple[int, int]]]
And a dataclass to store our detection results:
@dataclass(frozen=True)
class StageDetectorResult:
# create the data schema for the stage detector resulting, including
# the processed dataframe and the detected stages
df: pd.DataFrame
stages: DetectedStages
Now, let’s implement the main StageDetector class:
class StageDetector:
def __init__(
self,
df: pd.DataFrame,
fast_ma_size: int = 10,
slow_ma_size: int = 40,
min_consec: int = 4,
slope_window: int = 4,
rising_threshold: float = 0.0005,
falling_threshold: float = -0.0005,
flat_range: float = 0.0002
) -> None:
# store the input dataframe and fast and slow MA sizes
self.df = df
self.fast_ma_size = fast_ma_size
self.slow_ma_size = slow_ma_size
# store the minimum consecutive threshold to label a date range as a
# particular stage, along with the slope window used when calculating
# the slope of MA values
self.min_consec = min_consec
self.slope_window = slope_window
# store the trend thresholds
self.rising_threshold = rising_threshold
self.falling_threshold = falling_threshold
self.flat_range = flat_range
The constructor takes several parameters:
df: The DataFrame containing OHLCV data (assumed to be weekly data)fast_ma_size: The window for the fast moving average (default is10)slow_ma_size: The window for the slow moving average (default is40)min_consec: Minimum consecutive days to confirm a stage (default is4)slope_window: Window for slope calculation (default is4)rising_threshold: Threshold for considering a slope to be risingfalling_threshold: Threshold for considering a slope to be fallingflat_range: Range for considering a slope to be flat
Next, we’ll derive column names and initialize our stages dictionary:
# determine the fast and slow MA column names
self.col_fast_ma = f"{self.fast_ma_size}MA"
self.col_slow_ma = f"{self.slow_ma_size}MA"
# determine the slope column names
self.col_fast_ma_slope = f"{self.col_fast_ma}_slope"
self.col_slow_ma_slope = f"{self.col_slow_ma}_slope"
# initialize a dictionary to store the detected stages in the input
# dataframe
self.stages: DetectedStages = {}
Below we have the detect method of the class, which calls helper methods to identify each of the four stages:
def detect(self) -> StageDetectorResult:
# preprocess the dataframe by computing MAs and slope values
self._compute_indicators()
# detect each of the four stages
self._detect_stage_i()
self._detect_stage_ii()
self._detect_stage_iii()
self._detect_stage_iv()
# construct and return the stage detector result
return StageDetectorResult(
df=self.df,
stages=self.stages
)
This method orchestrates the detection process by computing indicators, detecting each stage, and returning the result.
Let’s implement the _compute_indicators method:
def _compute_indicators(self) -> None:
# compute the fast and slow MAs, then drop any NaN rows
self.df[self.col_fast_ma] = self.df["Close"].rolling(
window=self.fast_ma_size
).mean()
self.df[self.col_slow_ma] = self.df["Close"].rolling(
window=self.slow_ma_size
).mean()
self.df = self.df.dropna().copy()
# calculate slope for both the fast and slow MAs, dropping any NaN rows
# resulting from the calculations
self.df[self.col_fast_ma_slope] = self.df[self.col_fast_ma].rolling(
window=self.slope_window
).apply(calculate_slope)
self.df[self.col_slow_ma_slope] = self.df[self.col_slow_ma].rolling(
window=self.slope_window
).apply(calculate_slope)
self.df = self.df.dropna().copy()
This method calculates the fast and slow moving averages, as well as their slopes.
Now let’s implement the individual stage detection methods, starting with Stage I:
def _detect_stage_i(self) -> None:
# detect stage I conditions where (1) the fast MA is rising, (2) the
# fast MA is below slow MA, and (3) the slow MA is flattening out
idxs = np.where(
(self.df[self.col_fast_ma] < self.df[self.col_slow_ma]) &
(self.df[self.col_fast_ma_slope] > self.rising_threshold) &
(np.abs(self.df[self.col_slow_ma]) > self.flat_range)
)[0]
# update the stages dictionary
self.stages[Stage.STAGE_I] = find_consecutive_integers(
idxs,
min_consec=self.min_consec
)
The _detect_stage_i method identifies Stage I (Accumulation) by looking for three conditions:
- Fast MA is below the slow MA (price still below long-term trend)
- Fast MA is rising (short-term momentum turning up)
- Slow MA is flattening out (long-term trend stopping its decline)
Next comes our Stage II detector method:
def _detect_stage_ii(self) -> None:
# detect stage II conditions where (1) the fast MA is rising, (2) the
# fast MA is above the slow MA, and (3) the slow MA is also rising
idxs = np.where(
(self.df[self.col_fast_ma] > self.df[self.col_slow_ma]) &
(self.df[self.col_fast_ma_slope] > self.rising_threshold) &
(self.df[self.col_slow_ma_slope] > self.rising_threshold)
)[0]
# update the stages dictionary
self.stages[Stage.STAGE_II] = find_consecutive_integers(
idxs,
min_consec=self.min_consec
)
The _detect_stage_ii method identifies Stage II (Uptrend) by looking for:
- Fast MA above the slow MA (shorter-term trend stronger than longer-term)
- Fast MA rising (strong short-term momentum)
- Slow MA rising (confirming the longer-term trend is also up)
Similarly, we have Stage III:
def _detect_stage_iii(self) -> None:
# detect stage III conditions where (1) the fast MA is heading down,
# (2) the fast MA is still above the slow MA, and (3) the slow MA is
# flattening out
idxs = np.where(
(self.df[self.col_fast_ma] > self.df[self.col_slow_ma]) &
(self.df[self.col_fast_ma_slope] < self.falling_threshold) &
(np.abs(self.df[self.col_slow_ma]) > self.flat_range)
)[0]
# update the stages dictionary
self.stages[Stage.STAGE_III] = find_consecutive_integers(
idxs,
min_consec=self.min_consec
)
The _detect_stage_iii method identifies Stage III (Distribution) by looking for:
- Fast MA still above the slow MA (longer-term trend hasn’t reversed yet)
- Fast MA heading down (short-term momentum turning negative)
- Slow MA flattening out (long-term trend losing steam)
And lastly comes Stage IV detection:
def _detect_stage_iv(self) -> None:
# detect stage IV conditions where (1) the fast MA is below the slow
# MA, (2) the fast MA is down trending, and (3) the slow MA is also
# down trending
idxs = np.where(
(self.df[self.col_fast_ma] < self.df[self.col_slow_ma]) &
(self.df[self.col_fast_ma_slope] < self.falling_threshold) &
(self.df[self.col_slow_ma_slope] < self.falling_threshold)
)[0]
# update the stages dictionary
self.stages[Stage.STAGE_IV] = find_consecutive_integers(
idxs,
min_consec=self.min_consec
)
The _detect_stage_iv method identifies Stage IV (Downtrend) by looking for:
- Fast MA below the slow MA (shorter-term trend weaker than longer-term)
- Fast MA trending down (negative short-term momentum)
- Slow MA trending down (confirming the longer-term trend is also down)
I’ve also included what_stage, a helper method to determine what stage a specific date is in:
def what_stage(self, input_date: datetime) -> Optional[Stage]:
# grab the row index of the input date
row_idx = self.df.index.get_loc(input_date)
# loop over the computed stage indexes
for (stage_name, periods) in self.stages.items():
# loop over the starting and ending indexes for the period in the
# current stage
for (start, end) in periods:
# check to see if the input date index falls within this range
if start <= row_idx <= end:
# return stage name
return stage_name
# otherwise, no stage could be detected
return None
This method allows us to query what stage a specific date is in (assuming the date exists in our input DataFrame index).
Plotting our market stage detections #
This section covers creating a helper function to plot market stages on top of a candlestick chart.
Let’s start by defining a color scheme for visualizing our market stages:
# define default stage color mapping for visualization
DEFAULT_STAGE_COLORS = {
Stage.STAGE_I: "yellowgreen",
Stage.STAGE_II: "seagreen",
Stage.STAGE_III: "indigo",
Stage.STAGE_IV: "red",
}
Followed by Implementing a helper function to plot our market stage detections:
def plot_stage_detections(
stage_result: StageDetectorResult,
title: str,
stage_colors: Optional[Dict[str, str]] = None
) -> plt.Figure:
# check if the stage colors has not been supplied
if stage_colors is None:
# use the default stage colors
stage_colors = DEFAULT_STAGE_COLORS
This function takes a StageDetectorResult (i.e., the output of our .detect method detailed above), a title for the plot, and optionally custom stage colors.
Let’s now initialize a figure to plot our candlesticks and stage detections:
# initialize a new figure, then create a subplot for the stages
fig = mpf.figure(figsize=(14, 7), style="yahoo")
ax = plt.subplot(1, 1, 1)
# take the rectangle height to be the highest high in the dataframe
rect_height = stage_result.df["High"].max()
Plotting each stage is handled below:
# loop over the stages and periods
for (stage, periods) in stage_result.stages.items():
# loop over the periods in each stage
for (start, end) in periods:
# create a rectangle to visualize the stage
rect = patches.Rectangle(
xy=(start, 0),
width=end - start,
height=rect_height,
color=stage_colors[stage],
alpha=0.25
)
# compute the center x-coordinate of the rectangle and use it to
# draw the stage name inside the rectangle
cx = start + ((end - start) / 2.0)
ax.annotate(
str(stage.integer_value()),
xy=(cx, rect_height * 0.95),
color="black",
weight="bold",
fontsize=8,
ha="center"
)
# add the rectangle and text to the axis
ax.add_patch(rect)
ax.autoscale_view()
For each stage period, we create a colored rectangle spanning the duration of that stage and label it with the stage number.
And finally, we can construct our MA plots, finish constructing the figure, and return it to the calling function:
# create additional plots for the moving averages
addt_plots = [
mpf.make_addplot(
stage_result.df["10MA"],
color="royalblue",
ax=ax
),
mpf.make_addplot(
stage_result.df["40MA"],
color="maroon",
ax=ax
),
]
# plot the candlesticks with the MAs
mpf.plot(
stage_result.df,
ax=ax,
addplot=addt_plots,
type="candle"
)
# set the figure title and convert to a tight layout
fig.suptitle(title, fontsize=12)
plt.tight_layout()
# return the figure of stage detections
return fig
Examples of market stage detection #
Let’s see our stage detection system in action with some real-world examples:
# define the tickers we're interested in
tickers = ["SPY", "NVDA", "XOM"]
# set the start and end date of history requests
end_date = datetime(year=2025, month=3, day=7)
start_date = end_date - timedelta(days=365 * 4)
We’ll analyze three different tickers: SPY (S&P 500 ETF), NVDA (NVIDIA), and XOM (Exxon Mobil).
Given our tickers, let’s download market data for them:
# download market data for the tickers
df = yf.download(
tickers=tickers,
start=start_date,
end=end_date,
interval="1wk",
group_by="ticker",
auto_adjust=True,
progress=False
)
We download four years of weekly data for our analysis, which we’ll use in the upcoming sections.
S&P 500 (Stage II uptrend) #
Let’s apply our stage detector to the S&P 500:
# apply stage detection to the S&P 500
stage_detector = StageDetector(df["SPY"].copy())
result = stage_detector.detect()
Which will give us a DataFrame like the following:
# show the resulting dataframe
result.df
| Price | Open | High | Low | Close | Volume | 10MA | 40MA | 10MA_slope | 40MA_slope |
|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||
| 2021-12-27 | 450.419473 | 457.041327 | 450.371777 | 453.186523 | 279152600 | 442.683365 | 417.094993 | 2.301826 | 1.912733 |
| 2022-01-03 | 454.465051 | 457.976371 | 443.349125 | 444.723114 | 420356300 | 443.489420 | 418.751767 | 1.888487 | 1.905289 |
| 2022-01-10 | 441.488598 | 451.507250 | 435.668232 | 443.415985 | 448334500 | 443.282397 | 420.118907 | 0.930889 | 1.666164 |
| 2022-01-17 | 438.664236 | 438.874152 | 417.873171 | 417.901794 | 543717600 | 440.643765 | 420.711920 | -0.632582 | 1.221792 |
| 2022-01-24 | 412.224537 | 423.683974 | 401.471195 | 421.689789 | 920508000 | 438.229892 | 421.411914 | -1.841721 | 0.857345 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2025-02-03 | 590.892458 | 606.306112 | 588.719003 | 598.968201 | 216528100 | 595.479822 | 563.541061 | 1.061890 | 2.566275 |
| 2025-02-10 | 602.218421 | 609.157508 | 596.714958 | 607.871399 | 169013200 | 595.871527 | 565.880486 | 0.375613 | 2.378935 |
| 2025-02-17 | 609.047878 | 611.390805 | 597.672064 | 598.140686 | 170833900 | 595.647876 | 567.764099 | 0.096803 | 2.206632 |
| 2025-02-24 | 600.214463 | 601.221443 | 580.693169 | 592.397949 | 315266100 | 596.147662 | 569.504391 | 0.177987 | 1.977360 |
| 2025-03-03 | 594.391934 | 595.548489 | 563.933572 | 574.192688 | 416381600 | 594.244385 | 570.840652 | -0.438164 | 1.662079 |
Note how the DataFrame now includes our computed 10MA, 40MA, and their slopes. These values will be used to determine the market stages.
Speaking of which, let’s examine the detected stages:
# show the detected stages
result.stages
Which should give us the following output:
{<Stage.STAGE_I: 'stage_1'>: [(31, 38), (47, 53)],
<Stage.STAGE_II: 'stage_2'>: [(64, 89), (99, 165)],
<Stage.STAGE_III: 'stage_3'>: [(3, 9), (90, 98)],
<Stage.STAGE_IV: 'stage_4'>: [(17, 30), (39, 46)]}
The result is a dictionary where each key is a stage, and each value is a list of (start, end) index tuples indicating where that stage was detected.
We can visualize these stages using our plot_stage_detections method:
# plot the stages
fig = plot_stage_detections(result, "SPY Stages")

The chart shows:
- Stage III (distribution) in early 2022
- A drop to Stage IV (downtrend) in spring 2022
- Oscillation between Stage I (accumulation) and Stage IV as the market formed a bottom
- A strong Stage II (uptrend) starting in spring 2023
- A brief correction to Stage III in late 2023
- Continued Stage II growth through early 2025
This aligns perfectly with the actual market behavior during this period—the 2022 bear market, followed by the 2023-2025 bull run.
NVDA (Stage III decline) #
Now let’s analyze NVIDIA (NVDA), which experienced a massive bull run during this same period:
# apply stage detection to NVDA
stage_detector = StageDetector(df["NVDA"].copy())
result = stage_detector.detect()
# plot the stages
fig = plot_stage_detections(result, "NVDA Stages")

The NVDA chart shows:
- Similar early patterns to SPY with Stage III and IV in early 2022
- A strong Stage II (uptrend) starting in late 2022 through most of 2024
- Recent transitions between Stage III and Stage II
- Currently in Stage III (distribution phase)
This matches NVIDIA’s incredible performance during this period—up over 500% before showing signs of distribution in late 2024/early 2025.
XOM (Stage IV decline) #
Finally, let’s look at Exxon Mobil (XOM):
# apply stage detection to XOM
stage_detector = StageDetector(df["XOM"].copy())
result = stage_detector.detect()
# plot the stages
fig = plot_stage_detections(result, "XOM Stages")

The XOM chart reveals:
- A more complex pattern than the other examples
- Stage II (uptrend) in 2021-2022 during the energy boom
- Multiple transitions between stages
- Currently in Stage IV (downtrend)
This accurately depicts XOM’s mixed performance during this period, with strong gains during the energy crisis followed by underperformance as oil prices moderated.
Exercises #
Before we wrap up, try these exercises to reinforce what you’ve just learned:
Sector analysis: Apply the stage detector to different sectors (technology, healthcare, financials) to see how they behave relative to the broader market. Do certain sectors lead or lag the overall market in transitioning between stages?
Stage-based trading strategy: Implement a simple trading strategy that goes long in Stage II, takes partial profits in Stage III, and exits completely when Stage IV is confirmed. Backtest this strategy on several tickers and compare to buy-and-hold results.
Volume integration: Add volume analysis to complement the stage detection (volume often leads price). Create a scoring system that combines both price action and volume characteristics to strengthen your stage identification.
Final thoughts #
In this tutorial, you’ve learned how to implement Stan Weinstein’s market stage detection system using Python and Pandas.
This powerful tool helps you identify where a stock is in its market cycle—whether it’s building a base (Stage I), in a strong uptrend (Stage II), forming a top (Stage III), or in a downtrend (Stage IV).
By recognizing these stages, you can make more informed trading decisions, aligning your entries and exits with the natural flow of the market.
Remember, the goal isn’t to predict the future but to identify the current stage and adapt your strategy accordingly.
In the next tutorial, we’ll explore how to implement TradingView’s Stochastic RSI indicator in Python, another valuable tool for your trading toolkit.