Implementing TradingView's Stochastic RSI indicator in Python

Table of Contents
The Stochastic RSI indicator is a powerful tool for algorithmic traders looking to identify potential reversals and momentum shifts in the market.
The implementation we’ll be covering today tries to mimic the output you see in TradingView (as much as possible).
This tutorial is part 8 in a larger series on getting started with fintech and market analysis with Python:
- How to download market data with yfinance and Python
- Rethinking yfinance’s default MultiIndex format
- How to plot candlestick charts with Python and mplfinance
- How to compute Simple Moving Averages (SMAs) for trading with Python and Pandas
- Finding consecutive integer groups in arrays with Python and NumPy
- Computing slope of series with Pandas and SciPy
- Market stage detection with Python and Pandas
- Implementing TradingView’s Stochastic RSI indicator in Python (this tutorial)
- Introduction to position sizing
- Risk/Reward analysis and position sizing with Python
What is the Stochastic RSI indicator? #
The Stochastic RSI (StochRSI) indicator is a powerful technical analysis tool that might seem complex at first, but it’s actually built on two fundamental concepts that we can break down step by step.
Let’s start with the basics.
Technical indicators help traders analyze price movements to make more informed decisions.
While moving averages show us trends by smoothing out price data over time, momentum indicators measure the speed or strength of price movements.
The Relative Strength Index (RSI) is one of the most popular momentum indicators.
Developed by J. Welles Wilder in 1978, RSI measures the magnitude of recent price changes to evaluate whether an asset is potentially overbought (priced too high) or oversold (priced too low).
RSI outputs values between 0 and 100:
- RSI above 70 typically suggests an asset might be overbought
- RSI below 30 typically suggests an asset might be oversold
To identify potentially overbought or oversold assets, we compare the average gain to the average loss over a specific period (typically 14 days).
When prices rise strongly, RSI rises; when prices fall sharply, RSI falls.
The Stochastic Oscillator is another classic momentum indicator that compares a security’s closing price to its price range over a specific time period.
It helps identify when price momentum is slowing, even before this becomes apparent in the price itself.
The Stochastic RSI combines both the Relative Strength Index and Stochastic oscillator in a unique way.
Rather than applying the Stochastic formula to price data directly, it applies it to the RSI values themselves. This makes it a “momentum-of-momentum” indicator — essentially measuring the momentum of the RSI indicator.
By doing this, StochRSI becomes extremely sensitive to changes in market momentum, often providing earlier signals than either indicator alone could offer.
Specifically, StochRSI helps traders identify:
- When an existing trend might be losing steam before price reversal becomes obvious
- Potential turning points in the market with greater precision
- Short-term overbought/oversold conditions that traditional indicators might miss
Think of it as a magnifying glass for market momentum, allowing you to spot subtle shifts that could indicate trading opportunities before they become obvious to the average market participant.
How is Stochastic RSI calculated? #
Let’s break down the Stochastic RSI calculation into simple, digestible steps, starting from scratch.
Step 1: Calculate the standard RSI #
The foundation of the Stochastic RSI is the traditional Relative Strength Index (RSI).
To calculate RSI:
- Measure price changes: Calculate the difference between consecutive closing prices
- Separate gains and losses: Sort these price changes into upward movements (gains) and downward movements (losses)
- Calculate average gain and loss: Find the average gain and average loss over the specified period (usually 14 days)
- Calculate Relative Strength (RS): Divide the average gain by the average loss
- Convert to RSI: Apply the formula
RSI = 100 - (100 / (1 + RS))
This gives us a standard RSI value that fluctuates between 0 and 100.
Step 2: Apply the Stochastic formula to RSI values #
Instead of stopping with the regular RSI, we now take those RSI values and apply the Stochastic formula to them:
Stochastic RSI = (Current RSI - Lowest RSI) / (Highest RSI - Lowest RSI)
Where:
- Current RSI is the most recent RSI value
- Lowest RSI is the lowest RSI value over the specified lookback period (typically 14 days)
- Highest RSI is the highest RSI value over the same period
This normalization process creates a value that tells us precisely where the current RSI stands relative to its recent range:
- When the current RSI equals the highest RSI in the period, the Stochastic RSI equals 1 (or 100%)
- When the current RSI equals the lowest RSI in the period, the Stochastic RSI equals 0 (or 0%)
- When the current RSI is exactly in the middle of its range, the Stochastic RSI equals 0.5 (or 50%)
Essentially, we’re asking:
On a scale of 0 to 1, how close is the current RSI to its highest point over the lookback period?
Step 3: Apply smoothing for clearer signals #
Raw Stochastic RSI values can be extremely volatile, jumping rapidly between extremes.
To make them more practical for trading decisions, we apply two levels of smoothing:
The K-line: First, we calculate a simple moving average (SMA) of the raw Stochastic RSI values, typically over 3 periods. This creates our K-line, which is more stable than the raw values but still responsive to changes.
The D-line: Then, we calculate another simple moving average, this time of the K-line values (again, typically over 3 periods). This creates our D-line, which is even smoother and less prone to false signals.
This double-smoothing process creates two lines that frequently cross each other, providing potential trading signals:
- When the faster K-line crosses above the slower D-line, it might indicate a bullish signal
- When the K-line crosses below the D-line, it might indicate a bearish signal
The relationship between these lines and their position relative to the overbought (0.8) and oversold (0.2) levels provides traders with a comprehensive view of market momentum dynamics at a glance.
Stochastic RSI interpretation #
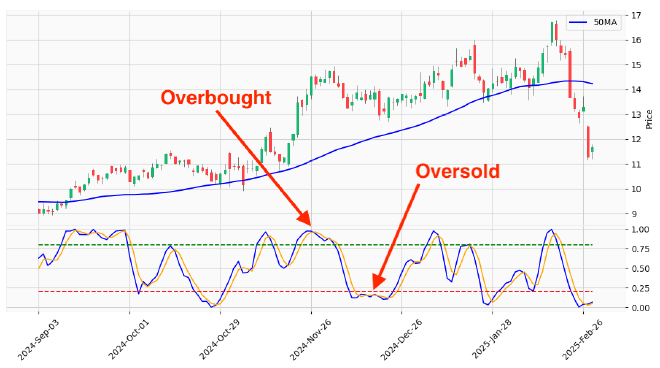
The Stochastic RSI provides several key insights for traders:
- Output Range: 0 to 1 (or scaled to 0 to 100), just like traditional stochastic indicators
- Signal Sensitivity: Since it’s built on RSI, which already filters raw price noise, StochRSI reacts faster than RSI and provides more frequent trading signals
- Overbought/Oversold Levels:
- > 0.8: RSI is near the top of its recent range → potential momentum exhaustion and reversal
- < 0.2: RSI is near the bottom of its recent range → potential reversal
When these key levels are breached, especially when combined with other confirmatory indicators or price action, they can signal high-probability trading opportunities.
Stochastic RSI Python implementations #
There are many variations and Python implementations for Stochastic RSI available to traders and analysts, including:
All of them have their slight variations, but effectively accomplish the same goal of calculating the Stochastic RSI indicator.
No implementation is “wrong”, but I prefer to have my Python output verify, as close as possible, what I see in TradingView, that way I’m seeing a consistent interpretation of the data across platforms.
The implementation I’ve provided today is based on ultragtx’s original GitHub gist.
My main contribution is to clean the code up a bit and explain what it’s doing under the hood, making it more accessible and educational.
Configuring your development environment #
Before we dive in, let’s set up our Python environment with the packages we’ll need:
$ pip install numpy pandas yfinance matplotlib mplfinance seaborn
These packages include:
- numpy: For efficient numerical operations and array manipulations
- pandas: For data manipulation and analysis through DataFrames
- yfinance: To download historical market data from Yahoo Finance
- matplotlib: For basic plotting capabilities
- mplfinance: For financial-specific visualizations like candlestick charts
- seaborn: For enhanced statistical data visualization
Implementing TradingView’s Stochastic RSI indicator #
Let’s get started by importing the required packages:
# import the necessary packages
from dataclasses import dataclass
from datetime import timedelta
from datetime import datetime
import mplfinance as mpf
import yfinance as yf
import pandas as pd
import numpy as np
Then we’ll define a StochasticRSIComputation class that will store the output of our calculations:
@dataclass(frozen=True)
class StochasticRSIComputation:
# define the data schema for stochastic RSI, including the raw values,
# K-line, and D-line
stoch_rsi: pd.Series
k_line: pd.Series
d_line: pd.Series
This class contains three key components:
stoch_rsi: The raw Stochastic RSI valuesk_line: The first smoothing of the raw Stochastic RSI (typically a 3-period moving average)d_line: The second smoothing, applied to the k_line (typically another 3-period moving average)
Next, we can define our actual stochastic_rsi function:
def stochastic_rsi(
series: pd.Series,
period: int = 14,
k_smooth: int = 3,
d_smooth: int = 3
) -> StochasticRSIComputation:
# check to see if an invalid period value was supplied
if period <= 0 or period >= len(series):
# raise an error
raise ValueError(
f"Period must be greater than 0 and less than the length of the "
f"series (got period={period}, data length={len(series)})"
)
Our function takes four parameters:
series: The price data series (typically closing prices)period: The lookback period for RSI calculation (default:14)k_smooth: The smoothing period for the K-line (default:3)d_smooth: The smoothing period for the D-line (default:3)
We perform some basic error checking to ensure the specified period is valid.
Now, let’s move on to calculating the price changes, separating them into positive and negative movements:
# calculate the price changes between consecutive periods, dropping any NA
# rows
delta = series.diff().dropna()
# initialize two series, one for price increases (ups) and another for
# decreases (downs)
ups = pd.Series(np.zeros(len(delta)), index=delta.index)
downs = ups.copy()
# fill the ups with positive price changes and the downs with absolute
# value of negative price changes
ups[delta > 0] = delta[delta > 0]
downs[delta < 0] = np.absolute(delta[delta < 0])
# set the first usable value as the average of the gains, removing the
# first period minus one values that aren't used
ups[ups.index[period - 1]] = np.mean(ups[:period])
ups = ups.drop(ups.index[:period - 1])
# do the same for the downs, setting the first usable value as the average
# of initial losses, removing any values that were not computed for a full
# period worth of data
downs[downs.index[period - 1]] = np.mean(downs[:period])
downs = downs.drop(downs.index[:period - 1])
This block of code implements the core logic for calculating RSI, which requires tracking price movements in both directions.
Let’s break down what’s happening line by line:
First, we calculate the price difference (
delta) between consecutive days by using the.diff()method. We immediately drop any NA values that result from this operation (the first row will always be NA since there’s no “previous day” for the first data point).Next, we initialize two separate series: one for upward price movements (
ups) and another for downward price movements (downs). Initially, both are filled with zeros and share the same index as our delta series.We then populate these series based on the direction of price movement:
- When prices increase (
delta > 0), we record the actual magnitude of the increase in theupsseries - When prices decrease (
delta < 0), we record the absolute magnitude of the decrease in thedownsseries (converting negative values to positive)
- When prices increase (
The critical part comes next: for the Wilder’s RSI calculation (which TradingView uses), we need an initial “seed” value. This is set at the
period - 1index position of both series by calculating the simple average of the firstperiodvalues.We then drop the first
period - 1values from both series since they’re not used in subsequent calculations. This ensures our data starts from the point where we have a full period’s worth of information.
This approach is specifically designed to match TradingView’s implementation of RSI, which follows Wilder’s original formula rather than the simplified versions found in some other implementations.
The careful handling of initial values and proper data alignment is crucial for getting results that match what you’d see on the TradingView platform.
Next, we’ll compute the exponential moving averages of ups and downs:
# compute the exponential moving average of the ups
ups_ewm = ups.ewm(
com=period - 1,
min_periods=0,
adjust=False,
ignore_na=False
).mean()
# do the same for the downs
downs_ewm = downs.ewm(
com=period - 1,
min_periods=0,
adjust=False,
ignore_na=False
).mean()
The exponential moving average (EWM) gives more weight to recent prices, making the RSI more responsive to recent market movements.
The com parameter (center of mass) determines the decay rate and is set to period - 1 to match TradingView’s implementation.
Now, we’ll calculate the Relative Strength Index (RSI):
# compute the relative strength (RS) as the average gains divided by the
# average losses, then construct the relative strength index (RSI) by
# scaling RS to the range [0, 100]
rs = ups_ewm / downs_ewm
rsi = 100 - (100 / (1.0 + rs))
# compute the stochastic RSI values using min-max scaling across the period
rsi_min = rsi.rolling(period).min()
rsi_max = rsi.rolling(period).max()
stoch_rsi = (rsi - rsi_min) / (rsi_max - rsi_min)
Here’s what’s happening:
- We calculate the Relative Strength (RS) as the ratio of average gains to average losses
- We convert RS to the Relative Strength Index (RSI) using the standard formula detailed above
- We then apply the stochastic formula to RSI by finding the highest and lowest RSI values in the specified period
- Finally, we apply min-max scaling to scale the RSI values to the range [0, 1]
Finally, we’ll smooth the results and return our computation:
# construct two smoothed values, including (1) the K-line, which is a
# smoothing of the raw stochastic RSI values, and (2) the D-line which
# is a smoothing of the K-line
k_line = stoch_rsi.rolling(k_smooth).mean()
d_line = k_line.rolling(d_smooth).mean()
# construct and return the stochastic RSI values (note that these values
# should be *very similar* to TradingView's implementation)
return StochasticRSIComputation(
stoch_rsi=stoch_rsi,
k_line=k_line,
d_line=d_line
)
The smoothing is applied in two steps:
- We create the K-line by taking a simple moving average of the raw Stochastic RSI values
- We create the D-line by taking a simple moving average of the K-line
This double-smoothing process reduces noise and provides clearer signals, reducing the likelihood of false positives.
Exploring our Stochastic RSI implementation #
We are now ready to test out our Stochastic RSI implementation on real market data:
# set the name of the ticker we want to download market data for
ticker = "RSI"
# set the start and end data for the history request
end_date = datetime(year=2025, month=3, day=1)
start_date = end_date - timedelta(days=250)
In this example, we’re using Rush Street Interactive (RSI) stock data (I thought it would be fun to use the RSI ticker for our StochRSI implementation) for the 250 days leading up to March 1, 2025.
Let’s fetch the market data:
# download OHLCV market data for the ticker
df = yf.download(
tickers=ticker,
start=start_date,
end=end_date,
interval="1d",
auto_adjust=True,
progress=False
)
# restructure the default multi-index dataframe to our preferred format
df = df.stack(level="Ticker", future_stack=True)
df.index.names = ["Date", "Symbol"]
df = df[["Open", "High", "Low", "Close", "Volume"]]
df = df.swaplevel(0, 1)
df = df.sort_index()
df.tail()
Which will result in a DataFrame that looks like the following:
| Price | Open | High | Low | Close | Volume | |
|---|---|---|---|---|---|---|
| Symbol | Date | |||||
| RSI | 2025-02-24 | 13.65 | 13.870 | 13.103 | 13.23 | 2139000 |
| 2025-02-25 | 13.09 | 13.210 | 12.630 | 12.89 | 2186700 | |
| 2025-02-26 | 13.14 | 13.730 | 13.140 | 13.30 | 2154600 | |
| 2025-02-27 | 12.50 | 12.562 | 11.160 | 11.27 | 7272800 | |
| 2025-02-28 | 11.50 | 11.790 | 11.200 | 11.66 | 3925800 |
The code above:
- Downloads OHLCV (Open, High, Low, Close, Volume) data for our specified ticker
- Restructures the data into a more intuitive multi-index format (as covered in this tutorial)
- Displays the last few rows of our dataframe
We’ll also compute a 50-day moving average to help visualize the trend:
# compute the daily 50MA
df["50MA"] = df.groupby(level="Symbol")["Close"].transform(
lambda x: x.rolling(window=50).mean()
)
The 50-day moving average is a popular indicator that helps identify the medium-term trend direction.
Computing Stochastic RSI on market data #
We are now ready to apply our stochastic_rsi function to the closing prices:
# compute TradingView's stochastic RSI indicator on the market data
stoch_result = stochastic_rsi(df.xs(ticker)["Close"])
Let’s add the calculated K-line and D-line values back to the original dataframe:
# set the location index into the dataframe to be the ticker and computed
# k-line index values
idx = (ticker, stoch_result.k_line.index)
# add the k-line and d-line values to the dataframe
df.loc[idx, "KLine"] = stoch_result.k_line.values
df.loc[idx, "DLine"] = stoch_result.d_line.values
# drop any NaN rows from the dataframe (caused by computing the MA and
# stochastic RSI values)
df = df.dropna()
df
Which should now look like:
| Price | Open | High | Low | Close | Volume | 50MA | KLine | DLine | |
|---|---|---|---|---|---|---|---|---|---|
| Symbol | Date | ||||||||
| RSI | 2024-09-03 | 9.19 | 9.240 | 8.990 | 9.02 | 1466200 | 9.4758 | 0.627819 | 0.491664 |
| 2024-09-04 | 9.04 | 9.420 | 8.924 | 9.18 | 1323500 | 9.4732 | 0.685669 | 0.609470 | |
| 2024-09-05 | 9.16 | 9.320 | 8.985 | 9.10 | 1351300 | 9.4692 | 0.535517 | 0.616335 | |
| 2024-09-06 | 9.10 | 9.210 | 8.930 | 9.08 | 973200 | 9.4638 | 0.586065 | 0.602417 | |
| 2024-09-09 | 9.17 | 9.530 | 9.140 | 9.39 | 1494800 | 9.4616 | 0.686873 | 0.602818 | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| 2025-02-24 | 13.65 | 13.870 | 13.103 | 13.23 | 2139000 | 14.3368 | 0.114241 | 0.268915 | |
| 2025-02-25 | 13.09 | 13.210 | 12.630 | 12.89 | 2186700 | 14.3246 | 0.000000 | 0.118716 | |
| 2025-02-26 | 13.14 | 13.730 | 13.140 | 13.30 | 2154600 | 14.3134 | 0.038610 | 0.050950 | |
| 2025-02-27 | 12.50 | 12.562 | 11.160 | 11.27 | 7272800 | 14.2654 | 0.038610 | 0.025740 | |
| 2025-02-28 | 11.50 | 11.790 | 11.200 | 11.66 | 3925800 | 14.2272 | 0.066729 | 0.047983 |
Our dataframe now includes:
- The original OHLCV data
- The 50-day moving average
- The Stochastic RSI K-line
- The Stochastic RSI D-line
We’ve also dropped any rows with NaN values, which occur at the beginning of our dataset due to the calculation requirements of our indicators.
Plotting Stochastic RSI indicator #
The final step is to visualize our data with a chart that includes:
- Price candles
- 50-day moving average
- Stochastic RSI K-line
- Stochastic RSI D-line
- Oversold level (0.2)
- Overbought level (0.8)
The oversold and overbought levels are particularly important as they help identify potential reversal zones:
- When the Stochastic RSI drops below 0.2, it suggests the asset may be oversold and due for a bounce
- Conversely, when it rises above 0.8, the asset may be overbought and due for a pullback
Below we create subplots for the 50MA, K-line, D-line, oversold line, and overbought line:
# construct additional plots
addt_plots = [
# plot the 50MA
mpf.make_addplot(
df.xs(ticker)["50MA"],
color="blue",
width=1.5,
label="50MA"
),
# plot the stochastic RSI k-line
mpf.make_addplot(
df.xs(ticker)["KLine"],
panel=1,
color="blue",
),
# plot the stochastic RSI d-line
mpf.make_addplot(
df.xs(ticker)["DLine"],
panel=1,
color="orange",
),
# plot the oversold line
mpf.make_addplot(
[0.2] * len(df.xs(ticker)),
panel=1,
color="red",
linestyle="--"
),
# plot the undersold line
mpf.make_addplot(
[0.8] * len(df.xs(ticker)),
panel=1,
color="green",
linestyle="--"
),
]
Finally, let’s create our visualization:
# plot the daily OHLCV bars, MA, and stochastic RSI
mpf.plot(
df.xs(ticker),
type="candle",
style="yahoo",
addplot=addt_plots,
figsize=(14, 7),
title=f"{ticker} - Stochastic RSI [Daily]"
)
The resulting plot should look like the following:
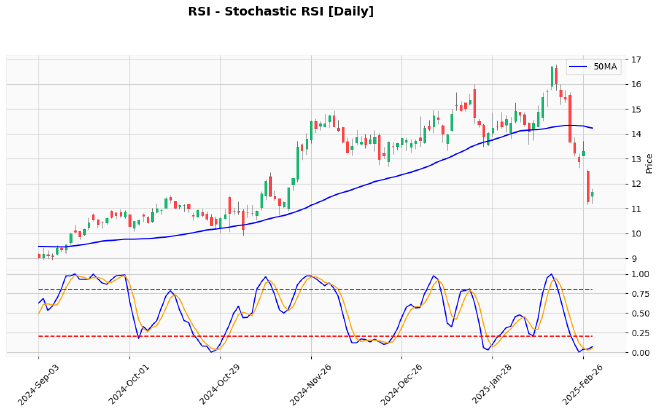
Looking at our chart, we can see:
- Rush Street Interactive (RSI) has been in a strong uptrend for much of the chart, as evidenced by price consistently staying above the 50MA (blue line) until the recent pullback
- The Stochastic RSI oscillates between the overbought (green dashed line) and oversold (red dashed line) levels
- Several trading opportunities presented themselves when the stock pulled back to the 50MA while the Stochastic RSI was in the oversold zone
For stocks in a strong Stage II trend (uptrend), the oversold line of the Stochastic RSI indicator becomes an extremely useful tool for timing entries.
Good times to buy are when we see confluences between the moving average and Stochastic RSI:
- Price comes down to the 50MA, slightly touching or bouncing off it (typically on high volume)
- At the same time, Stochastic RSI is showing oversold conditions (below 0.2)
When these conditions align, there’s often a higher probability of the stock resuming its upward trend. Typically, you would buy during this time and place a stop loss just below the 50MA.
While this isn’t a perfect strategy by any means, it’s an important tool in a swing trader’s arsenal for identifying potential entry points with favorable risk/reward profiles.
Exercises #
Before we wrap up, try these exercises to reinforce what you’ve just learned:
Parameter optimization: Experiment with different period settings for the Stochastic RSI (try 7, 14, and 21 days) and different smoothing values for the K and D lines. Analyze how these changes affect the sensitivity and reliability of the signals. Which parameters work best for different market conditions?
Multi-indicator confirmation: Combine the Stochastic RSI with the 50MA and standard RSI to create a rule-based entry system. For example, only enter long positions when price is above the 50MA, RSI is above 50, and Stochastic RSI is moving up from an oversold condition. Backtest this system on several tickers.
Divergence detection: Write code to automatically detect divergences between price and Stochastic RSI. These occur when price makes a new high while Stochastic RSI makes a lower high (bearish divergence), or when price makes a new low while Stochastic RSI makes a higher low (bullish divergence). These divergences often precede significant reversals.
Final thoughts #
In this tutorial, we’ve implemented TradingView’s Stochastic RSI indicator in Python.
We’ve explored the calculation methodology, created a clean and reusable implementation, and visualized the results on real market data.
The Stochastic RSI combines the strengths of two powerful momentum indicators (Relative Strength Index and Stochastic oscillator), providing traders with a more sensitive tool for identifying potential reversals and overbought/oversold conditions.
When used alongside other technical analysis tools like moving averages, it can help pinpoint higher-probability entry and exit points.
Remember that no indicator is perfect, and Stochastic RSI should be used as part of a comprehensive trading strategy that includes proper risk management and position sizing.
In the next tutorial, we’ll dive into the critical topic of position sizing and how it can dramatically impact your trading results.